For experts.

All the following equations and parameters are described in the Theory page.

During geological time, if the climate becomes wetter, by how much does the altitude of the mountain decrease?

This question has been the subject of a famous controversy (e.g. Molnar and England, 1990; Whipple et al., 1999; Dielforder et al., 2020). This is known to be a complicated problem that depends on the co-evolution of precipitation with altitude and rainfall variability (Roe et al., 2003; Lague, 2014). Let’s keep it simple and look at what happens if the rains are constant and homogeneous. By comparing the maximum altitudes for simulations (those with m = 0.5 and n = 1) with different values of precipitation rate P, we find that the maximum altitude zmax ~ P^-0.9. This means that if P is multiplied by 2, the mountain relief will be divided by about 2 (a bit less). Can we predict this result?

For that, we can try to predict the relationship between the slope and P at dynamic equilibrium, when the erosion rate balances the tectonic uplift rate. The mountain relief is actually the integral of slopes along river path, but the resulting scaling with precipitation is the same as long as P is homogeneous.

If we neglect hillslope processes (only rivers) and lateral erosion, the mass balance equation is

At dynamic equilibrium, the elevation does not change anymore and thus

Replacing the erosion and deposition rates by their formulae (see Theory page) we obtain

where Q [L³/T] is the volumetric water discharge. For homogeneous precipitation rate P, Q = PA where A is the drainage area. At dynamic equilibrium, we can also write Q_s = AU, namely the sediment outflux balances the tectonic flux. Then, rearranging the pieces, we obtain The last equation has the form of the well known ”Slope-Area relationship” (S = k_sA^-θ). It links the local slope S and a power law of the local drainage area A for every pixel of the model grid.

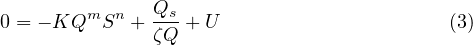
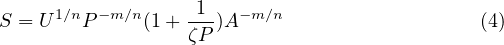
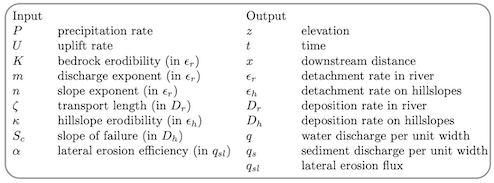
Thus, in simulations with m = 0.5 and n = 1, the slope S scales with P^-0.5(1 + ).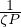

As explained in the Theory page, ζ si proportional to the reverse of the settling velocity of transported grains in rivers, and thus is larger for finer sediment grains. This is true for an ”instantaneous” description of sediment transport (Davy and Lague, 2009) but in LEMs, ζ is an apparent parameter that captures also periods without transport, as explained in the Data Repository of Guerit et al. (2019). If the climate corresponds to rare and short floods, ζ increases.

What does a high ζ value imply? In the case that ζ >> 1, the previous slope-rainfall scaling reduces to S ~ P^-0.5, ie. the slope scales with the reverse of the squared rainfall rate. In other words, when P is multiplied by 2, S is only divided by 1.4. And if ζ is very low? In that case, if ζ << 1, S ~ P^-0.5(1 + 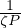) ~ P^-1.5. The scaling that we found by plotting the maximum elevation of the mountains for different rainfall P (S ~ P^-0.9) lies between these two end-member cases.

The value ζ = 1 used in these simulations is indeed intermediate and it is therefore not surprising to find a scaling law that is also intermediate.

Rmq: A large ζ >> 1 makes the deposition term D_r in Equation 1 very small (because D_r = Qs∕ζQ). It can be negligible compared to the detachment rate term ϵ. This means that once a particule of the riverbed is detached, it is transported and deposited eventually very far, after a very long transport distance larger than the total river length. This is the definition of a ”Detachment-limited” river system in geomorphology. On the contrary, if ζ << 1, then D_r becomes significant and any particle detached from the riverbed will have a non-negligible probability of redeposition at close range. This is the definition of a ”Transport-limited” river system, because the variation of the riverbed elevation depends on the capacity to carry sediment rather than to detach particules. Detachment and Transport-limited systems have very different predictions in terms of transient river behaviour. Experts can learn more by reading Whipple and Tucker (1999, 2002). The product Pζ determines the very detachment or transport limited nature of rivers and of the whole landscape. Values Pζ > 1 tend to generate detachment-limited river topographies whereas Pζ < 1 tend to generate transport-limited topographies. Natural systems tend to have a large range of Pζ values but with a significant proportion with Pζ ≤ 1 (towards transport-limited behaviour). Experts can learn more by reading Davy and Lague (2009); Guerit et al. (2019).

Conclusion? Yes the model prediction is consistent with the underlying theory (ufff). The theory predicts that a simple parameter changes a lot the scaling between mountain elevation and rainfall. This parameter depends on the size of transported grains. This is a nice example of how the characteristic of a small ”nothing” (sediment particule) potentially determines the morphology of a big thing (the whole landscape). It remains to be understood what controls the size of grains transported by rivers. There is an important, poorly explored consequence: if Pζ is small then S ~ P^-1.5. In that case, for low P values, ie. arid climate, a small change in P has a dramatic effect on S. For wetter climates with larger P the change is on the contrary modest.

Obviously, this is not all the story. This analysis holds for m = 0.5 and n = 1, it must be reevaluated for other values. In particular, accounting for detachment threshold in the ϵ detachment law and for the full range of floods in rivers changes things. Experts can learn more by reading Tucker (2004); Lague (2014); Deal et al. (2017). Vegetation and most probably glaciers play a role too.

And what about the scaling with tectonic uplift rate U? Look at the simulations and verify the predictions of the theory using the same approach as above.

Suggestions for teaching:
Discuss the predictions for different m and n values.
Discuss the limitations of the model concerning the analysis of the S-P scaling (constant and homogeneous rainfall rate, no weathering, no vegetation, no glaciers, only one grain size, realism of the dynamic equilibrium hypothesis, response time of topography to a change in P etc...)
Discuss how to test these predictions on natural examples using Google Earth and global climate data.

References